Journal d'un Terrien
Web log de Serge Boisse
On line depuis 1992 !
Si cette page vous a plu, Copiez son adresse et partagez-la !
http://sboisse.free.fr/technique/spatial/Calculs pour le lancement d'une fusee.php
Auteur: Serge Boisse
Date: Le 27/11/2023 à 20:11
Type: MOC/technique/astronautique
tags:
- technique
- astronautique
- fusée
- spatial
- mécanique
- espace
aliases:Tout ce que vous voulez savoir sur les fusées spatiales sans oser le demander, ou "les fusées pour les nuls"
Résumé :
On va essayer de retrouver par le calcul les grandes lignes du design d'une fusée bi-étage, par exemple la fusée falcon 9 de la société SpaceX. Au passage, on fera un petit cours (très simple) de mécanique orbitale !

Petit rappel
Pour lancer un satellite, il ne suffit pas que la fusée monte "suffisamment haut". Il faut surtout que le second étage et la charge utile acquièrent une vitesse horizontale suffisante pour que la charge utile tourne autour de la terre sans retomber du fait de la gravité.
Cette vitesse doit être au minimum de 8 km/s, soit 28000 km/h. Pour cette raison, la fusée, initialement verticale, va monter certes, mais surtout s'incliner de plus en plus à l'horizontale. Il peut même arriver qu'à un moment donné son altitude diminue légèrement (sur une trajectoire quasi horizontale) pour gagner de la vitesse ! Le calcul montre que parfois c'est rentable de faire ainsi !
La force de gravitation
L'altitude h de la fusée est sa hauteur au dessus de la surface de la Terre, que nous supposerons sphérique. Pour le calcul des orbites, toutefois ce n'est pas pratique et on utilisera plutôt la distance
L'avantage d'utiliser
G est la constante de gravitation universelle de Newton, M est la masse de la terre en Kg, m est la masse de la fusée en Kg encore, et
Le résultat
Cette formule vous fait peur ? En fait elle dit juste que la force de gravitation
Cette force attraction entre deux objets a une intensité
Mais cette force est très faible, sauf si la masse de l'un des objets est très grande. C'est pourquoi il y a cette constante
En revanche, si l'un des "objets" est la Terre, qui a une masse énorme
Dans la pratique, si on fait des calculs pour une fusée partant de la Terre, on utilisera la constante
Pour information, l'unité de GM que nous utilisons ici et dans la suite est le
Ce paramètre
Exemple
Ainsi, au niveau du sol, un objet ayant une masse de 1 kg subit donc une force d'attraction vers le bas de
Eh oui, il va falloir faire la différence entre le poids, qui est une force, et la masse, qui est une caractéristique immuable de l'objet.
La masse se mesure en grammes ou en kilogrammes (ou en tonnes, etc.) mais le poids, comme toutes les forces, se mesure en Newton (
Le poids varie selon l'emplacement, mais pas la masse.. Un objet qui a une masse de 1 kg, et qui pèserait 9,81 N à la surface de la Terre, ne pèse que 1,62 N sur la Lune !
A l'altitude de 200 km, on a
Vitesse orbitale
Eh oui, presque autant que les 9,81N à la surface de la Terre ! Pour que le satellite ne retombe pas, il doit aller très vite horizontalement, pour créer ainsi en tournant autour de la terre une force centrifuge qui compensera la force d'attraction terrestre.
Comment calculer cette vitesse ? La force centrifuge qui s'exerce sur un corp de masse
Eh oui, si vous faites tourner autour de vous une corde de longueur
Cette force
Rappelez-vous que les forces se mesurent en Newton et les masses en kg, et que un objet de masse 1kg pèse 9,81 N à la surface de la Terre !
Donc, pour que le satellite reste en orbite, il lui faut au minimum une vitesse
On écrit juste ici que pour que le satellite reste en orbite circulaire, il faut que l'attraction terrestre
Si on est fûté, on va donc pouvoir calculer la vitesse minimale pour qu'un satellite reste en orbite à la distance
En simplifiant, on trouve
Ouh la la, il y a une racine carrée
Pas de panique ! Regardons ce qu'il y a en dessous : GM est une valeur constante, donc
Donc plus un satellite est haut (
soit, numériquement dans notre exemple d'un satellite à 200 km d'altitude :
Le job d'une fusée n'est donc pas tant d'aller très haut que d'aller très vite !
Les bases de la propulsion spatiale
En propulsion spatiale, la grandeur la plus importante est le
Donc
Changement d'orbite
Pour passer d'une orbite circulaire à une autre, généralement plus haute, on démontre que la méthode la plus économique est de passer par une orbite intermédiaire, elliptique (en forme d'ellipse), appelée orbite de transfert
Les orbites elliptiques sont caractérisées par deux points particuliers :
- Le périgée est le point de l'orbite le plus prés de la Terre
- L'apogée est le point de l'orbite le plus éloigné de la terre
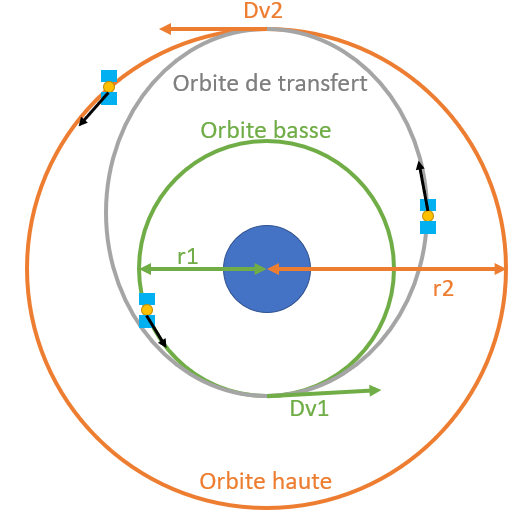
On fait donc une première poussée au périgée (en bas sur l'image), ce qui nous met sur l'orbite de transfert, puis une seconde poussée une fois parvenu à l'apogée, ce qui circularise enfin l'orbite.
Les
Vous trouverez ici : https://i.imgur.com/WGOy3qT.png une carte complète des
Par exemple pour passer d'une orbite circulaire à une altitude de 200 km à une autre orbite circulaire à 500 km d'altitude, le calcul donne
En revanche pour attendre l'orbite géostationnaire, située à une altitude de 35 786 km, et toujours à partir de notre orbite "basse" à 200 km d'altitude, il faut un
La formule de Tsiovolsky
Pour une fusée loin de la terre en, en négligeant donc les frottement atmosphériques, et en l'absence de toute force externe, ce
Bon, ça veut dire quoi cette formule ? Voyons voir : Pour calculer la différence (mais en fait c'est l'augmentation) de vitesse
le log est une fonction croissante, donc plus ce rapport est grand (c'est à dire plus on a consommé de carburant), plus la fusée gagnera en vitesse. Logique, non ?
Ca, va, vous suivez toujours ? On a fait le plus dur !
Ainsi en définitive la vitesse finale atteinte par une fusée ne dépend que de la vitesse
La vitesse d'éjection des gaz dépend des ergols utilisés et de l'efficacité des moteurs : les deux combinaisons d'ergols les plus utilisées sont le mélange oxygène/hydrogène liquides (le plus efficace avec une vitesse d'éjection maximale de 4 462 m/s) et le mélange kérosène/oxygène liquide (vitesse d'éjection maximale de 3 510 m/s.
La formule de Tsiovolsky peut être aussi utilisée "à l'envers" pour déterminer le rapport des masses initiales et finales en fonction de la vitesse des gaz et du
ou, de manière équivalente,
Avec bien sûr
Enfin, si les moteurs ont un débit d'ergol constant,
Et puisque
Le décollage
Pour un décollage vertical, il faut modifier un peu la formule de Tsiovolsky comme suit, pour prendre en compte le freinage dû à la pesanteur :
où
est la durée de la poussée (sensée supérieure au poids total de la fusée !)
Encore une formule ! Mais n'ayez pas peur ! Celle-ci n'est en fait rien d'autre que La formule de Tsiovolsky un peu modifiée : elle nous permet de calculer la vitesse acquise par la fusée pendant qu'elle monte, mais cette fois en tenant compte du fait qu'elle doit "s'arracher" à la gravité terrestre qui la freine.
Si vous la regardez bien, vous noterez un terme supplémentaire
On comprend l'intérêt qu'il y a d'obtenir la plus grande poussée possible au décollage, ceci pour minimiser le temps T et donc le freinage dû à la gravitation.
Enfin, lorsqu'une fusée décolle du sol jusqu'à la hauteur
où
est l'accélération locale (moyenne) de la pesanteur. Comme nous l'avons vu, pour des orbites basses, celle-ci varie très peu avec l'altitude, et pour simplifier on peut prendre une valeur moyenne.
En intégrant le terme de freinage
Mais en fait la fusée doit s'incliner progressivement au cours de la montée. Donc il existera un angle
Enfin, si la fusée a déjà une composante de vitesse horizontale importante, il faut tenir compte de la force centrifuge, qui cette fois va aider la fusée.
Et bien sûr comme l'angle
Cela semble compliqué, mais en fait, non ! : en effet, si on suppose que l'angle varie d'une manière continue de 0 à 90 degrés au cours de la poussée, ce qui n'est pas très éloigné de la réalité, nous sommes sauvés car
Exemple : Fusée monoétage
Par exemple pour une fusée à un seul étage, avec lancement à partir du sol (
Si la la vitesse
donc
Il faudrait donc que la fusée soit 18 fois plus légère une fois son carburant épuisé ! Puisque la masse initiale
C'est quasiment impossible à réaliser, et c'est pourquoi toutes les fusées existantes sont des fusées à plusieurs étages.
Et encore, on a négligé ici le frottement atmosphérique, qui réduirait encore le
Le frottement atmosphérique et la résistance de l'air
Bien sûr, une fusée est très rapide, et la force aérodynamique augmente comme le carré de la vitesse. Mais d'un autre côté, la densité de l'air diminue très vite avec l'altitude, et sa vitesse initiale est ... zéro. Il existe donc un point, que l'on appelle
En fait, Une fusée est assez aérodynamique, et l'influence de tout ceci sur le
Donc bien moins que la perte de vitesse due à la gravité !
Le site de Lancement
Paradoxalement, le choix du site de lancement peut nous aider : en effet, La terre tourne ! En 24h, elle fait un tour sur elle même, autrement dit, un point sur l'équateur aura tourné de 40070 km, qui est la circonférence de la planète.
Cela représente une vitesse de 40070/24 = 1670 km/h, ou en encore 463 m/s : ce n'est pas négligeable, et si nous tirons vers l'Est, cette vitesse viendra s'ajouter à la composante horizontale de la vitesse de la fusée, autrement dit se retrancher du
Si nous tirons vers l'Ouest, en revanche, il faudra ajouter ces 463 m/s à notre
Et si le site de lancement n'est pas sur l'équateur ? Eh bien, si sa latitude est L, notre "bonus" en tirant vers l'Est sera tout simplement
A Kourou, on bénéficie d'un bonus de 461 m/s, contre 327 à Toulouse, 407 à Cap Canaveral en Floride, 439 à Boca Chica au Texas (site de lancement des starship), et seulement 217 à Baïkonour.
Les moteurs
Le rôle du moteur fusée est de jeter le plus de masse possible et plus le vite possible vers l'arrière de la fusée, ce qui par réaction propulsera la fusée vers l'avant, suivant la loi de conservation de la quantité de mouvement.
On pourrait penser que la caractéristique la plus importante d'un moteur de fusée est sa poussée, mais c'est inexact. Pour les spécialistes, les deux chiffres les plus importants dans la conception d'un moteur sont son impulsion spécifique" et son débit massique. Késako ?
Le débit massique
Le débit massique souvent noté
Contrairement aux réacteurs des avions, les fusées n'utilisent pas l'oxygène de l'air, elles transportent leurs propres reserves dans d'immense réservoirs, en plus du carburant.
L'impusion spécifique
Pour déterminer l'efficacité d'un moteur fusée, on utilise l'impulsion spécifique qui se mesure en seconde, et qui est la durée pendant laquelle un kilogramme de propergol produit la poussée nécessaire pour élever une masse d'un kilogramme dans le champ gravitationnel terrestre au niveau du sol (c'est à dire une force de 9,81 N). Cette impulsion spécifique
Par définition, donc :
Où
et
Par conséquent, la vitesse
Par exemple pour un moteur ayant une impulsion spécifique de 360 secondes, ce qui est le cas des moteurs
Ce qui permet de réécrire la formule de Tsiovolsky (3.1) en fonction de l'impulsion spécifique du moteur :
Bon, si vous êtes arrivés jusqu'ici, vous ne devriez plus être perdus.
A partir de l'équation d'origine (3.1)
Comme, pour un moteur donné,
Souvenez-vous que cette formule permet de calculer la vitesse finale atteinte par la fusée en l'absence de toute force extérieure. C'est donc super important !
Comment déterminer la poussée d'un moteur fusée ?
Si on connait la vitesse d'éjection des gaz, et le débit massique
Si la tuyère est conçue de telle façon que
Mais c'est impossible dans le vide puis que alors
Fusée à deux étages, non réutilisable
On appellera
La masse au décollage de la fusée est donc la somme de toutes ces masses :
On mesurera les masses en kilogrammes ou en tonnes .
On supposera que les deux étages ont des moteurs d'impulsion spécifique respectives
Le premier étage propulse l'ensemble jusqu'à la vitesse
Cette vitesse finale théorique doit être supérieure à la vitesse orbitale de 7,9 km/s (cf. eq. 2.3),
Les deux étages ont des rôles, et donc des profils de vol, très différents.
Le rôle du premier étage est de monter le plus haut possible et le plus vite possible, tout en s'inclinant de plus en plus à l'horizontale.
Donc dans le calcul de
Le second étage, en revanche doit accélérer horizontalement, c'est à dire sans presque monter, de manière à communiquer au satellite une vitesse suffisante pour... le satelliser, of course.
Donc dans le calcul de
Le premier étage monte jusqu'à la hauteur
où
Eh, oh, n'ayez pas peur ! C'est juste une fraction avec au dessus les différent termes qui déterminent la masse totale au décollage, et en dessous la masse finale de la fusée une fois son carburant épuisé (juste avant le largage du satellite)
En fait, comme ce premier étage fonctionnera en grande partie dans l'atmosphere, le
Si le moteur du premier étage a fonctionné pendant le temps
Le second étage, quant à lui, fournira un incrément de vitesse qui est :
avec
Les choix à faire lors de la conception
Il faut alors faire quelques hypothèses sur la conception de la fusée. On essayera de la faire la plus légère possible, et de maximiser la quantité de carburant embarquée.
Il faut aussi choisir le ratio de masse entre le premier et le second étage.
Par exemple pour la fusée Falcon 9 on a, en tonnes :
| Masse vide | carburant | total | % total | durée | |||
|---|---|---|---|---|---|---|---|
| premier étage | 25,6 | 395 | 420,6 | 78% | 3,74 | 300s | 162s |
| second étage | 3,9 | 92,6 | 96.5 | 18% | 4,57 | 348s | 397s |
| charge utile | 22 | 22 | 4% | ||||
| TOTAL | 539,1 | 100% |
On constate que la structure d'une fusée est très légère. La masse du premier étage est constitué à 94% de carburant, celle du second (sans la charge utile) à 96%, ce qui est énorme, mais cela tombe à 21% si on inclut la charge utile.
Enfin, le second étage plein et avec sa charge utile représente 22% de la masse totale. Si l'on prend en compte uniquement les structures vides, celle du second étage ne représente que 13,2 % de la masse totale. Pourquoi ce choix ? Parce que le premier étage, le plus lourd, sera abandonné en route et qu'un second étage relativement leger pourra alors accélérer "à fond, à fond, toujours à fond", comme dirait Alain Prost.
De la théorie à la pratique
Nous pouvons alors calculer nos
Pour le premier étage,
Pour le second,
Soit un
page créée le 06/12/2023 à 19:25modifiée le 10/01/2024 à 20:28
Commentaires (0) :
Page :Ajouter un commentaire (pas besoin de s'enregistrer)
En cliquant sur le bouton "Envoyer" vous acceptez les conditions suivantes : Ne pas poster de message injurieux, obscène ou contraire à la loi, ni de liens vers de tels sites. Respecter la "netiquette", ne pas usurper le pseudo d'une autre personne, respecter les posts faits par les autres. L'auteur du site se réserve le droit de supprimer un ou plusieurs posts à tout moment. Merci !Ah oui : le bbcode et le html genre <br>, <a href=...>, <b>b etc. ne fonctionnent pas dans les commentaires. C'est voulu.